What is a Low-Pass Filter and How Does it Work?
![]()
Most digital cameras from the 2000s and 2010s are equipped with an optical element called an optical low-pass filter (OLPF), also known as an anti-aliasing (AA) or blur filter. As the name “filter” suggests, this optical element filters out some information coming from the imaged scene.
In this article, we will explain why removing higher spatial frequencies might be of interest to a photographer, how the optical low pass filter does so, and why most modern cameras no longer use them.
Table of Contents
Low-Pass Filters in Digital Cameras
If you have ever photographed a scene or object with certain fabrics and/or a grid-like pattern, you may have noticed that the resulting photo contains an unwanted (possibly rainbow-colored) effect in those areas.

The colorful effect can often result when photographing certain types of clothes and/or fabrics.

This effect is due to moiré patterns and false color, and it occurs when repetitive lines or patterns exceed the resolution of the image sensor.

To combat unwanted moiré patterns and false color in photos, camera manufacturers designed optical low-pass filters and placed them over image sensors. This camera feature can greatly reduce or eliminate the amount of moiré interference seen in photos.
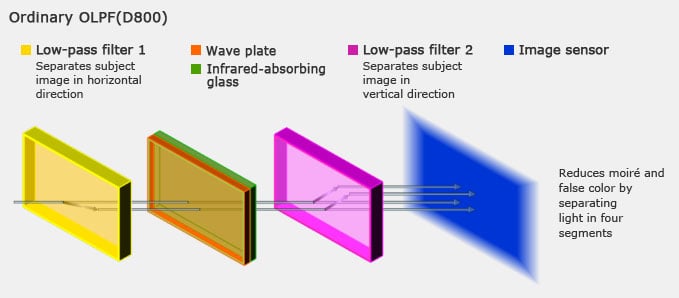
By ever-so-slightly blurring the ultra-fine details of a scene, low-pass filters became ubiquitous in digital cameras as the solution to moiré.
This tactic does come with a tradeoff, though: the price for less moiré is slightly less sharpness. For the vast majority of photographers, particularly casual ones using their cameras for everyday snapshots, the difference in sharpness is imperceptible, so the inclusion of a low-pass filter is a no-brainer.
However, for some photographers who do need the ultimate level of sharpness in their photos — landscape photographers and astrophotographers, for example — the blur introduced by a low-pass filter may be undesirable. Moiré patterns are almost always found in manmade things, so those shooting nature on the ground or in the sky typically have no need for a low-pass filter. These photographers may elect to purchase a camera that leaves out the low-pass filter or they may have their cameras modified to remove the filter from in front of the sensor.
Many of the latest digital cameras in the industry also leave out the low-pass filter in favor of increased sharpness, but more on that later.
Spatial Frequencies 101
Now that you understand the high-level basics of low-pass filters and moiré patterns, let’s dive deeper into the science behind how it all works.
Before we can understand why we should use any sort of spatial resolution filter on the camera sensor, let us first explain some basic concepts regarding signal processing. Fundamentally, a 2D image can be decomposed into a sum of sinusoidal waves with different amplitudes and frequencies.
Although a mathematical proof of it would be far beyond the scope of this article, this property is used in many image processing algorithms or image compression formats. To get a sense of the frequency content of an image, one can compute a Fourier transform of it, using the 2D-FFT algorithm.
It is possible to try this algorithm online with your own images. The center of any 2D Fourier transform comprises the low spatial frequencies of the image whereas the edges contain the high spatial frequencies, namely the fine details of the image.

From a mathematical viewpoint, taking a perfect picture requires a proper estimation of all the spatial frequencies from the object scene. In practice, the worst that could happen to the image content is that some spatial frequencies are lost or recorded with wrong information through the imaging process.
Since the image resolution is finite, there is by definition a maximal spatial frequency that can be recorded, which is sensor related. This is known as the sensor “Nyquist frequency”. Any spatial frequency above this maximal frequency simply cannot be recorded, in the same way, that one cannot count 30 with only 10 fingers. The estimation of this highest spatial frequency recorded depends on the Nyquist-Shannon sampling theorem. This theorem states that for a given frequency f (in cycles/mm), one needs to acquire at least twice the number of points per cycle. A direct formula should look like this:
![]()
When available, this formula is further enriched with information about the pixel shape and display through the Kell factor. The Nyquist spatial frequency of most sensors is usually around 100 cycles/mm.
Filtering Out the Moiré Artifacts
Now that we have established the theoretical maximal spatial frequency of an image sensor, a new question arises: what happens to all the higher spatial frequencies?
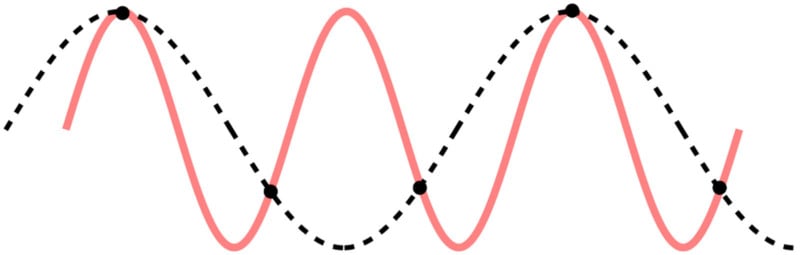
These higher spatial frequencies do not simply vanish through the imaging process, they are recorded incorrectly because of the low number of samples available. Since they cannot be recorded with the correct high frequency, they are incorrectly recorded with a much lower spatial frequency. This effect is known as aliasing or moiré patterns.
It might be interesting to highlight that this property of moiré patterns can be seen on test charts (Imatest charts, for instance). On such test charts, any spatial frequency above the peak resolution of the system will result in either plain gray blur or moiré patterns (usually diagonal lines).

Needless to say, moiré patterns are unpredictable and far from visually pleasing. They also tend to be quite difficult to correct algorithmically. Even state-of-the-art algorithms using neural networks often fail with real-life images since moiré patterns tend to exhibit color artifacts as well. Those color artifacts appear since the moiré pattern might be different for the red, green, and blue channels recorded by the camera.

How Are Optical Low Pass Filters Made?
In order to avoid the various moiré artifacts and patterns listed above, engineers have tried to adjust the optical resolution of the system to match the sensor. If the optical system limits the resolution, instead of the sensor, higher frequencies are blurred out and do not create artifacts on the final image.
A very practical problem comes with this idea of a lens with voluntarily limited resolution. This technically means that each lens must be tailored for a specific sensor resolution. In fixed lens systems, such as smartphone cameras, this is easily achievable. However, in DSLRs or mirrorless systems, lenses must be compatible with several generations of sensors. Optical Low Pass Filters find an elegant solution to the problem. Using a thin optical filter placed directly on the sensor, one can adjust virtually any lens to match the sensor’s resolution.
Still, blurring the image with the desired amount of blur is a technical challenge. Ideally, one would like the filter to be uniform across the sensor (field invariant), consistent regardless of the focal length (chief-ray angle invariant), and uniform for all colors (color invariant).

The most common technology used to build low-pass filters relies on birefringence, most commonly with the use of birefringent quartz. To quote Wikipedia: “Birefringence is the optical property of a material having a refractive index that depends on the polarization and propagation direction of light”. To simplify it further, in such materials, the light path differs depending on the light polarization.
Since visible light is made up of at least vertical and horizontal polarized light, after traveling into a birefringent material, two slightly shifted images are produced. The process is then repeated, layer after layer of birefringent material, in order to produce additional shifted images. A typical DSLR filter contains two layers of birefringent material.
Why Low-Pass Filters Are Disappearing from Cameras
Since the 2010s, optical low-pass filters have been removed from DSLRs. The removal trend started with the Nikon D800 released in 2012. This flagship Nikon camera was sold both with or without an optical low pass filter (as Nikon D800 and Nikon D800E variants), assuming that photographers would pick the most suitable camera for their needs. In real-life, reviewers found the difference subtle, in most situations.
Removing the low-pass filter has three main reasons, according to manufacturers. First, the sensor resolution has increased dramatically since the first digital cameras, which enabled higher frequency information to be recorded.
Second, as stated earlier, very high-frequency information is quite rare in nature, which means that the risk of having moiré in a picture tends to decrease as the image resolution increases.
Third, digital image processing has improved and can correct images if need be.
Maybe an even bigger shift explains the lack of low-pass filters. Contrary to the 2000s, lenses are increasingly the limiting factor when it comes to resolution, as opposed to sensors. Finding a lens outperforming a 50MPx sensor is quite difficult, even with an unlimited budget. In practice, this means that most lenses act as optical low-pass filters by themselves.
There is still a large community requiring low-pass filters: the video community. Although video resolution has increased from 720p to 4K in the past decade, moiré artifacts are still fairly common and low pass filters play a role. After all, 4K is still around 8 megapixels, which is close to the still-image resolution of the late 2000s. RED cameras, for instance, offer some physical OLPF or a digital correction. Until 8K video becomes the norm, optical low-pass filters, or at least the “bloom filters”, should remain useful for videographers.
About the author: Timothee Cognard is an optical expert and photographer based in Paris, France.
Image credits: Header illustration made with photo by Phiarc and licensed under CC BY-SA 4.0